Shops, Trade, and Banking Stabilizers

Following onto the discussion of Caiani et al. and their stock-flow consistent model, this week I turn to Ashraf, Gershman, and Howitt, who develop a model of shops, trade and banks to show that the presence of bank lending during times of crises leads to better overall macroeconomic performance. More precisely - the more risky the bank's lending approach (higher loan-to-value ratio) the better the outcome. The caveat, these banks are very secure as their failure does not have substantial real economic effects.

My intrigue when looking at this set of ABM studies was twofold. The first thing that caught my eye is that the firm entry (or shop-opening) process was more realistic than some other ABMs I have read. Entrepreneurs choose to start a firm themselves, rather than new firms coming in to replace firms that have gone bankrupt. The second, eye-catching feature was their main results: the increase in stability outweighs the financial accelerator mechanism of the stylized financial system. This went against my intuition, which has been shaped by the literature on systemic risk in the financial sector and other readings about the 2008-2009 financial crisis.

The Turnstile of Firm Entry and Exit

The aspect of this model that caught my eye immediately was the protocol for firm entry. Specifically, the detail of the decision-making process of whether to start a new shop, as well as generation of a business plan based on estimated profits. This is much closer to what one would imagine an entering firm to consider. To summarize, the process looks somewhat like the following picture

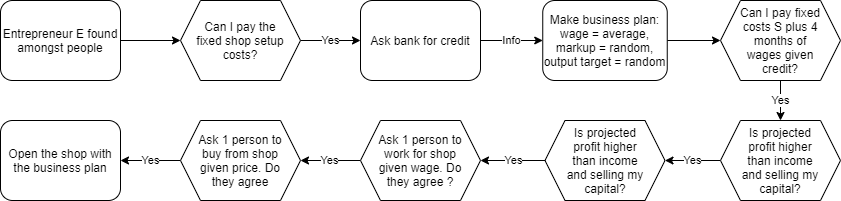
Why is this particularly interesting? Firstly, the number and concentration of firms becomes an endogenous property of the model. There is no longer a fixed number N of firms that compete, such that if a firm fails, an "identical" firm replaces them. Rather, this could allow for interesting studies of market-concentration, entry of new firms, the size of the markets over time. There is one limiting factor to this, namely that the distribution of desired goods is constant. Nonetheless, as wealth shifts between individuals, demand shifts, and so would the opportunity for new firm entries (low demand = not a good moment).

The second reason this is interesting is that the startup capital and value of the firm is independent. In other models where bankrupt firms are simply replaced by an entrant, the firm sizes are often simply retained. In this case, the new firm's size solely depends on the wealth of the founder and the credit that she can get. Similarly the size evolution of the firm depends on how well it can attract labour and customers with its decisions on wages and prices of goods.

In their results, Ashraf et al. do touch on several aspects of firm entry, though through the lens of bank-lending. Specifically, how the number of shops, failures of financial viability to start a new show, and the number of new entrants differ in the presence of different types of banks. I would be interested about "survivorship" of shops, what the determinants of the survival are, and what the size-distribution of shops is. Perhaps this isn't the ideal model to study firm dynamics per se, after all, a firm seems much more complicated than a shop.

Banks: Crisis Accelerators or Stabilizers?

Most of the recent discourse I have come across is about how the financial system, or bank lending, is an accelerator. In other words, the financial system can accelerate downturns and make our system more unstable. In this paper, Ashraf and co-authors show that the reverse is true in their model economy. Their main reasoning is as follows:

by financing replacement firms and additionally supporting existing ones in the event of an adverse shock, banks confer a stabilizing influence on macroeconomic performance, and this influence is most noticeable in worst-case scenarios. In this respect, banks in our model provide a financial stabilizer that more than counteracts the familiar financial accelerator

So how come banks are so beneficial? In my opinion it is because in these models banks are particularly safe, there is almost no risk for the bank. What I mean is if a bank faces bankruptcy, then the government will fully re-capitalise the bank and give ownership to the richest non-owner depositor in the bank. All deposits are preserved, loans are unaffected, other banks are unaffected, the government has filled up the equity to ensure the capital adequacy ratio is met. In essence, bank failure, other than for the owner, appears to be uneventful, without repercussion.

For banks with positive equity that fail to meet capital adequacy requirements, there is a sanction. Namely, no new loan issuances or dividend payments. This becomes the financial friction in the model. Due to the fact that the bank essentially cannot act to earn higher interest on new loans, it must hope that the firms it has loaned too do not face bankruptcy. In this way, credit availability has become sparser. However, if a firm does fail and equity becomes negative, the bank experiences a reset to full lending capacity (at least for one turn) such that it can again make loans.

The key factor for banks is the loan-to-value ratio, which prescribes how much they are allowed to lend. The higher the ratio, the more a bank may lend, the more risky the bank is (it is easier to become troubled).

How does this translate? Ashraf et al. show that in their simulations there is a worst-case. They split runs into deciles according to the average output gap. The highest decile performs markedly worse than the others, and there appears to be a particular kink in the distribution.

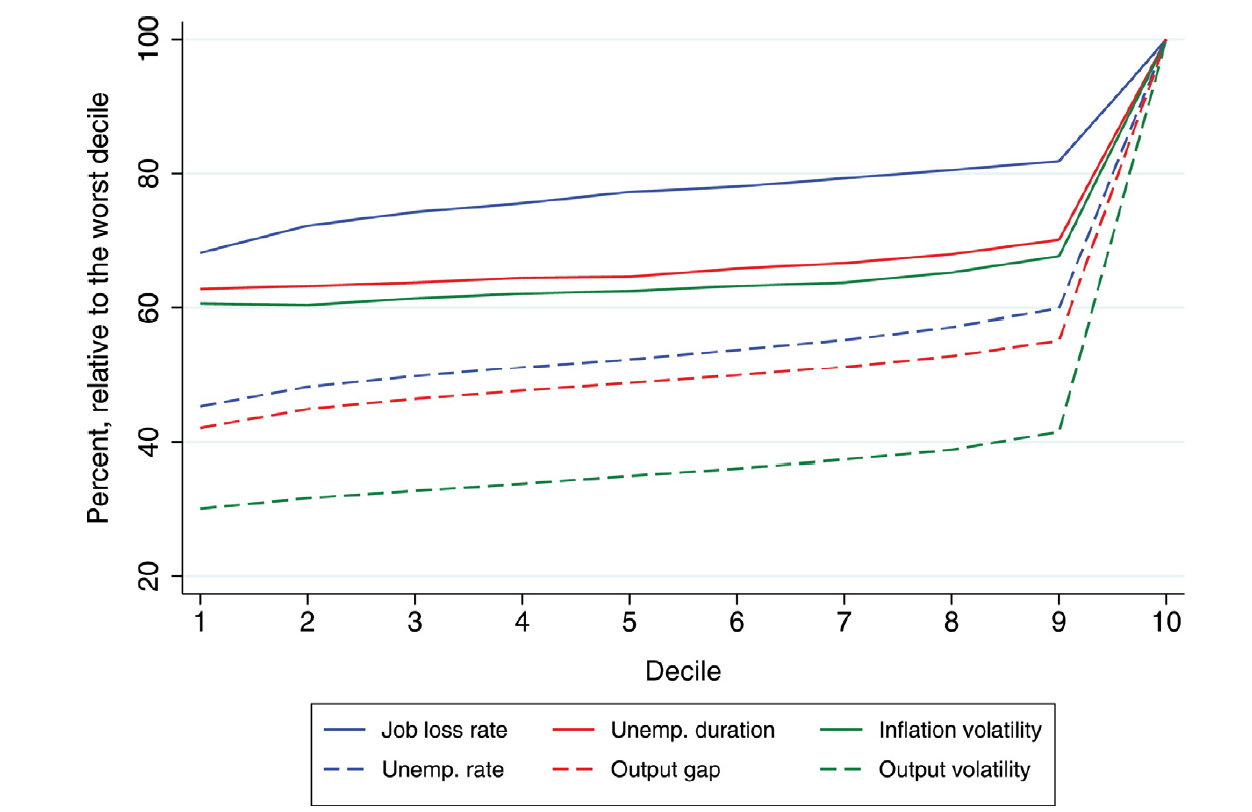
The remainder of their paper studies how the presence and riskiness of banks affect overall performance, and in particular the top decile's performance. They reach the conclusion that banks' presence improves the economic situation, and furthermore that more risky banks (higher loan-to-value ratio) is even more beneficial to macroeconomic performance. Their reasons are as follows:

One reason for our finding that risky banks improve macroeconomic performance in the worst decile is that their higher failure rate does not impinge negatively on the real economy

Suggesting that perhaps one should take the increased stability results with a grain of salt, as the negative of bank behavior may be understated (see the large literature on systemic financial risk...)

In a robustness check, Ashraf and colleagues contend that introducing crooks (borrowers with no intention to repay) does not change their results. The reason for introducing crooks is that "One argument for believing that bank failure does in fact impair macroeconomic performance is that it may result in the loss of important information that the failing bank had regarding its customers." The effect of this introduction is that it now takes time for new customer relationships to be established, in the sense that there will be a much higher interest rate charged in the period just after a bank is "rescued".

Their results for this check is to say that overall macroeconomic performance decreases across the board in the presence of crooks. However, risky banks (those with a higher loan-to-value ratio) still lead to better outcomes than the cases without, or with safer banks. The reason remains the same:

While tighter lending standards make little difference in normal scenarios, in worst-case scenarios, the economy exhibits significantly weaker performance under more stringent regulations(such as higher capital requirements or lower loan-to-value ratios), because these regulations suppress the lending activity that is especially needed during a rare disaster.

Overall - I see the benefit to the existence of banks that will lend during crises thus creating more stability (or at least a less drawn-out crisis). I would add to their result that these banks, much as in their cited study by Coleman and Feler (2015), are very secure. The results of Coleman and Feler suggest that the areas where government banks continued to lend as private banks reduced credit had better employment outcomes during the crisis.

Validation

Since my own research primarily focuses on the empirical validation of agent-based models, I am curious about how this particular model is validated.

In the paper, a three-level procedure for calibrating parameters is suggested:

1. Parameters are chosen based on their empirical counterparts or on values used in previous studies (in this case some parameters are based on prior DSGE models for the time-preference, which does not seem entirely sound. Those models are fundamentally different, and those parameters were found by fitting the models. How do we know the same notion is even applicable here? Most keenly because agent-behavior is no longer rational forward-looking optimisation at the aggregated level, but non-forward looking individual decisions at the micro-economic level)
2. The values of other parameters are chosen to be internally consistent with median outcomes across simulations. (To be clear - this mostly refers to setting initial values and targets for government predictions on the median outcomes of simulations.
3. Remaining parameters were loosely picked to resemble properties of U.S. economic data. In particular, they essentially replicate the seminal Stock & Watson (1999) econometric study that is a standard reference for most stylized facts. Furthermore the triad of relationships often observed is replicated (Delli Gatti et al. 2011 do so), namely: the Philipps curve, Okun's law, and the Beveridge curve

Overall, the validation is in-line with what is common in ABMs - taking parameters from the data directly and matching stylized facts where possible - to achieve Level 1 validity (see my post here).

What else has happened?

A fun quirk about this particular model is that the follow-up paper of the model was published before the model itself was published. It was on arXiv for almost five years (2011 on arXiv, 2017 it was published).

To the best of my knowledge there are only two directly related papers:

1. In How inflation affects macroeconomic performance: an agent-based computational investigation Ashraf, Gershman and Howitt investigate the effects of changes in "trend inflation" on their model. Specifically, inflation is not uniform but dispersed across prices (some large hikes, some small ones), which can lead to coordination failures
2. In 2017, Popoyan et al. published Taming macroeconomic instability: Monetary and macro-prudential policy interactions in an agent-based model which extends the model of Ashraf by considering bank balance sheets and macroprudential regulation. They assess the effects of the Basel III regulations on the macroeconomy and of different monetary policy rules.

Verdict

I enjoyed the simplicity in which the model is presented as people opening shops and taking out loans. Furthermore, the alignment of the model with DSGE-type equilibrium models meant that under some conditions Ashraf et al. were able to determine what the steady state of the system was. This is quite interesting, as often it is unclear about whether or not agent-based models ever reach a steady state. While there are statistical means of testing this, computationally it might be much too intensive.

The overall aim of the model, to demonstrate that the bank-stabilising effect can outweigh the financial accelerator effect of banks is intriguing. However, given the very safe banking system presented here it should be taken with a grain of salt. I do think that to make the claim more robust, the banks themselves should be modelled in more detail (as in Popoyan et al. proceed to do) to account for behavior such as reduced credit availability in crisis or the way that banks are interlinked amongst each other (cascades in the banking system) that may have a dampening effect.

References and Notes

** Cover photo by Tim Evans on Unsplash

Ashraf, Q., Gershman, B., & Howitt, P. (2016). How inflation affects macroeconomic performance: An agent-based computational investigation. Macroeconomic Dynamics, 20(2), 558–581. https://doi.org/10.1017/S1365100514000303

Ashraf, Q., Gershman, B., & Howitt, P. (2017). Banks, Market Organization, and Macroeconomic Performance: An Agent-Based Computational Analysis. Journal of Economic Behavior and Organization, 135, 143–180. https://doi.org/10.1016/j.jebo.2016.12.023

Coleman, N., & Feler, L. (2015). Bank ownership, lending, and local economic performance during the 2008–2009 financial crisis. Journal of Monetary Economics, 71, 50–66. https://doi.org/10.1016/j.jmoneco.2014.11.001

Popoyan, L., Napoletano, M., & Roventini, A. (2017). Taming macroeconomic instability: Monetary and macro-prudential policy interactions in an agent-based model. Journal of Economic Behavior & Organization, 134, 117–140. https://doi.org/10.1016/j.jebo.2016.12.017